Attacking Electronic Codebooks

Introduction

In this blog post we will discuss weaknesses in the Electronic Codebook (ECB) block cipher mode of operation and demonstrate an attack on a very general implementation of AES operating in ECB mode. This can hopefully serve both as evidence to dissuade the use of ECB mode for the purpose of protecting data, and provide a starting point for security researchers and penetration testers to build their own proof-of-concepts targeting implementations of ECB mode in the wild.

AES Overview

The Advanced Encryption Standard (AES) Is a symmetric-key block cipher. To briefly review what this means: The terms symmetric-key and block cipher both describe cryptographic primitives which are distinct building blocks of the AES cipher. Firstly, ciphers which make use of symmetric-key algorithms employ the same key for both enciphering plaintext and deciphering the resulting ciphertext, as opposed to different keys for each respective operation. Next, the term block cipher describes a category of ciphers for which the input to the main cryptographic transformation is a group of bits 2ⁿ long. To put this another way: if you wanted to encrypt a single word, a block cipher would transform the entire word at once, whereas a stream cipher would transform each letter one at a time.

Electronic Codebook Mode Overview

The main limitation of a block cipher when considered as a primitive is that a message must be equal in length to the defined block size, so what if we want to transform messages that are too small to fill an entire block? What if the message is too large to fit inside a feasible power of two? If a message is too short, we can simply pad the message with garbage data until it is the correct length. If a message is too long, we will, at minimum, need to run our block cipher more than once, which leads us into block cipher modes of operation. Block ciphers have a variety of “modes” which govern how the single block transformation of the cipher will be executed in repetition for messages that exceed the block size. The simplest of these, and the focus of this blog post is Electronic Codebook (ECB) mode. ECB mode divides the message into blocks and each block is transformed independently of every other block using the defined key.

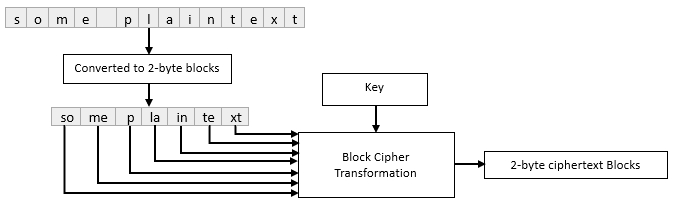
To understand the inherent weakness in this method, we must consider the role of entropy or randomness in cryptosystems. At their core most ciphers are deterministic, which means when given a specific input they will always produce the same output. In other words: equivalent plaintext inputs will always result in equivalent ciphertext outputs. The trouble with deterministic encryption schemes is that any patterns which are present in the plaintext will be present in the ciphertext, for example if we were to encrypt a series of emails from the same sender, the blocks containing the email signature should always be equivalent, which can give a cryptanalyst their foothold. There are two main solutions to this problem: A bad one and a good one. The bad solution would be to regenerate the key for every block. This would produce non-equivalent ciphertext outputs for equivalent plaintext inputs, however deciphering a message of any length could require hundreds or thousands of keys which, because we’re using a symmetric key algorithm, both sender and recipient would need a copy of every key. The good solution is to implement and additional input to the main cryptographic transformation that defines it’s initial state: A random or pseudo-random value called an Initialization Vector which is meant to make each block of ciphertext distinct regardless of the plaintext. ECB mode’s lack of randomization creates the basis for the attack described in the next section of this blog post and represents the main reason why it should never be used to protect data.

Below is an example contrasting ciphertexts produced deterministically using ECB mode and ciphertexts which have been randomized with an initialization vector using Cipher Block Chaining (CBC) mode. All ciphertexts are transformations of the same word: “Secret” in a 16-byte block.

The Attack

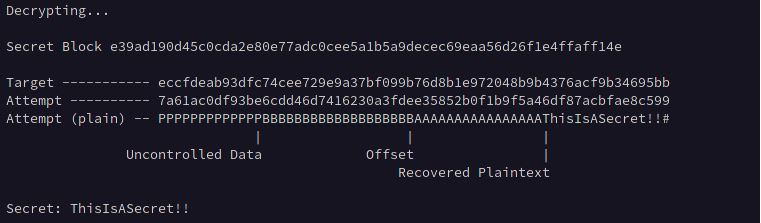
To illustrate the weaknesses of ECB mode we will execute an adaptive chosen-plaintext attack on a string of data encrypted using AES operating in ECB mode. The rough scenario we’ll use to demonstrate this is a token which contains a secret along with some data we control. This could be thought of as a web token, encrypted application data or anything else, the only prerequisite for executing this attack is the ability to obtain the ciphertext for semi-arbitrary plaintexts.

Determining Block Size

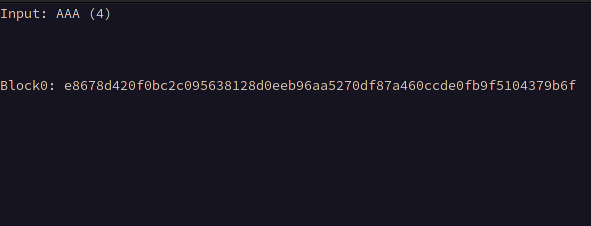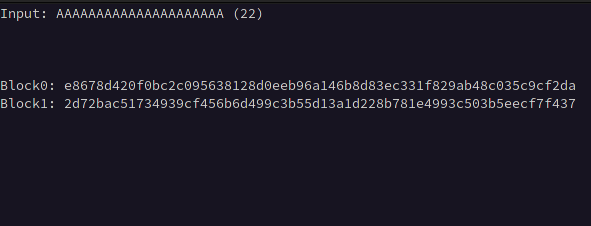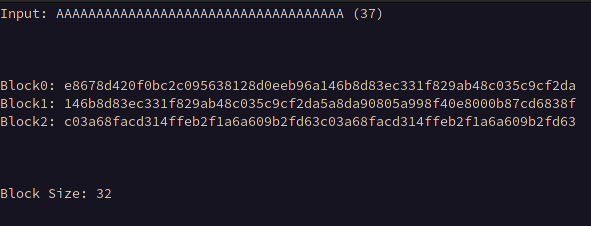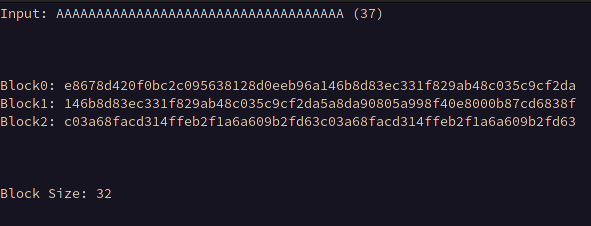
The first step is determining the block size used by the cipher, this will allow us to determine where our input begins and ends, We can calculate this by first taking the initial ciphertext length with minimal input such as a single character, then incrementing the length of our input by one until the ciphertext doubles in length, suggesting the length of the ciphertext has exceeded one block, then continue incrementing the length of our input until the ciphertext triples in length, then subtract the length of the input observed at the time the ciphertext doubled in length from the length of the input observed when it tripled in length.

For example, if the ciphertext length doubled at an input of 5 characters and tripled at 37, we subtract 5 from 37 giving us the block size of 32.

Determining Offset

It is unlikely that that our chosen plaintext will be inserted at the first byte of the first block, so it is necessary to calculate the input length required to offset any prepended data to align with the block boundary. This can be accomplished by prepending bytes in increasing length to a static value equal in length to the block size * 2 until two identical consecutive blocks of ciphertext are observed.

For example, if we know the block size is 32, we can input 64 A characters, which will create identical 32-byte blocks when that data is exactly split across two blocks.

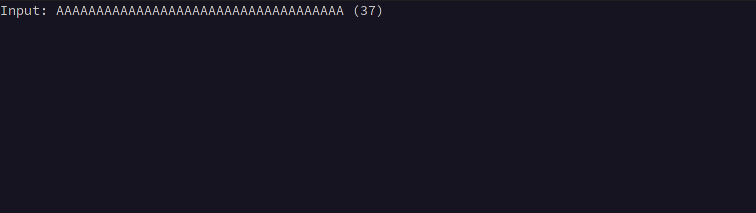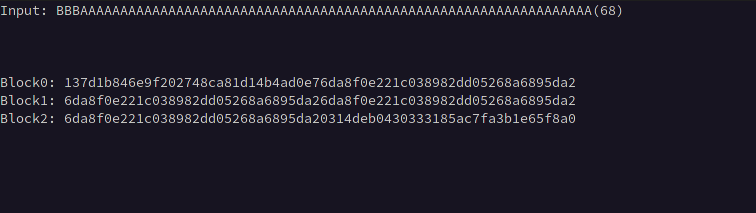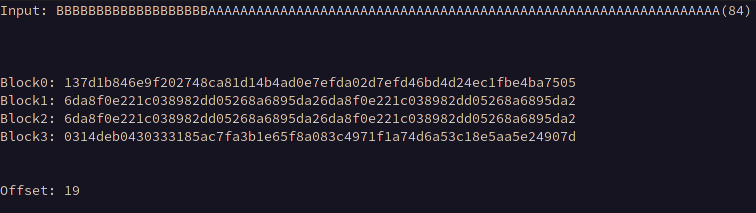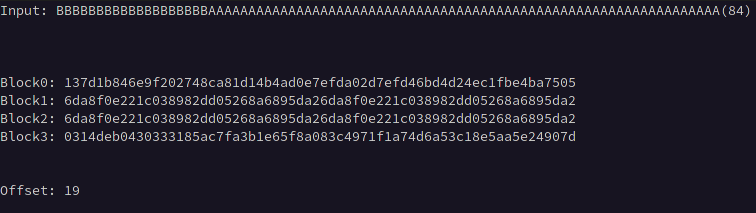
Below we can see blocks 1 and 2 become equivalent after prepending 19 B characters to the 64 A characters indicating that our offset is 19 bytes.

Brute Forcing

Now that we control the exact position of the secret in the ciphertext we can submit an input of offset + block size – 1 which will populate the last byte of the last block containing our input with the first byte of the secret which we record as our target value, and brute force the character by iterating through all possible values for the plaintext and comparing the result with our target value.

Once our attempt matches the target value, we record the character used and then submit an input of offset + block size + recovered plaintext character – 2 and record that as the target value, then iterate through all possible values for the second byte of the secret and so on until it is entirely recovered.

Conclusion

Like all practical attacks on modern cryptosystems, the example detailed above targets an insecure implementation of the AES cipher rather than the cipher itself which is, as of writing, absolutely a secure method of maintaining the confidentiality of information. However, as this example illustrates, any given cipher is only as secure as its implementation.

Sauce

The code used to demonstrate & visualize the attack can be found at: https://github.com/ra5ca1/ECB-attack-demo